Poisson’s Ratio in Thermodynamics – Derivation | Wiki

It may seem a little difficult to understand Poisson’s Ratio in thermodynamics, but don’t worry! We are going to simplify it for you so that it can be easily understood by you.

When an elastic strap is stretched out, have you ever noticed that it becomes thinner as it extends longer? Poisson’s Ratio in Thermodynamics provides an explanation about the context of science and energy, in a way!

We’ll discuss Derivation for Poisson’s Ratio, its significance, and its relationship to thermodynamics—the study of heat, energy, and motion and change—in this blogpost. Together, let’s explore and learn the mysteries of Poisson’s Ratio in thermodynamics!

A rubber or elastic band that is stretched will get longer and have a smaller diameter. This is caused by the fact that when you pull on something, it decreases in one direction in addition to stretching in another. Poisson’s Ratio has something to do with this concept!

This article will discuss Poisson’s Ratio and its relationship with thermodynamics, the science that describes the transformation of heat and energy. 

These words may seem a little difficult right now, but do not worry about it. We’ll walk through all of them and discuss how scientists apply mathematics to make sense of these amazing changes in materials.

Poisson’s Ratio in Thermodynamics

When you squeeze a ball of playdough, it expands outwards to accommodate your pressure. On the other hand, consider pulling on a rubber band; as it lengthens, the middle of the band becomes thinner.

Poisson’s Ratio, which helps us understand how materials respond when forces are given to them, is connected with these form changes.

What is Poisson’s Ratio?

A measurement known as Poisson’s Ratio indicates how much a material shrinks when stretched or thickens when compressed.

A piece of clay, for an example, may expand out in length but also narrow on the sides if you push on it. Scientists can precisely determine how much a material thins or thickens when forces are applied to it by using Poisson’s Ratio.

We compare a material’s stretch in one direction to its shrinkage in another direction to find Poisson’s Ratio. A rubber band that has been stretched to a very thin point has a high Poisson’s Ratio.

The Poisson’s Ratio is lower if the thickness doesn’t fluctuate significantly.

What Does Thermodynamics Have to Do With Poisson’s Ratio?

The branch of chemistry or physics that describes the movement of energy and heat is known as thermodynamics.

Materials can expand or contract in response to extreme temperatures or cold, much like a balloon does when air that is heated is injected into it.

The Poisson’s Ratio of a material can also be influenced by how it responds to temperature variations.As for an example, when  a metal bar is heated to a high temperature it may grow both in length and width.

Scientists can better understand how substances react to temperature changes by using thermodynamics in addition to forces like stretching and compressing.

Heat has the ability to alter a material’s shape and size in a variety of ways by affecting the motion of its molecules.

These may also help you:

Biochemistry Analyzer Uses and Principle: A Comprehensive Guide

Haloalkanes and Haloarenes Handwritten Notes | Class 12

Structure of Atom Class 11 PPT

50 Examples Of Balanced Chemical Equations With Answers

Positive Deviation From RAOULT’S LAW – Explaination – Solution

A to Z Body Parts Name | Human Body Parts that Starts

Why Poisson’s Ratio Matters in Thermodynamics?

Knowing Poisson’s Ratio in thermodynamics is necessary for a variety of applications, including construction and designing structures as well as the development of fresh components for automobiles and aircrafts.

Engineers are able to create robust, secure, and dependable objects by understanding how materials react to stresses and temperature changes!

Derivation for Poisson’s Ratio in Thermodynamics

We use equations that describe how energy flows through a material when it is stretched, compressed, or heated to get Poisson’s Ratio in thermodynamics.

We can determine the link between strain (the amount of change) and stress (the force applied to the material) using these equations. By using thermodynamics, we may better understand the relationship between Poisson’s Ratio and the internal energy of the material.

In other words, Poisson’s Ratio explains how objects expand and compress, while thermodynamics clarifies the energy underlying those changes!

This is how it operates:

We quantify the amount that the material lengthens (or contracts) in response to an applied force. We refer to this as longitudinal strain.

Additionally, we quantify the amount of breadth variation, or lateral strain.

To put it simply, Poisson’s Ratio is the ratio of these two values. The calculation looks like this:

Poisson’s Ratio= − ^{Lateral Strain​}/_{Longitudinal Strain}

How to Derive Poisson’s Ratio in Thermodynamics: A Comprehensive Guide

In thermodynamics, Poisson’s Ratio can be derived (or calculated) using the following fundamental concepts:

• The amount that an object varies in configuration when forces such as stretching or compressing are applied is called strain. A “lateral strain” refers to how much it shrinks, and a “longitudinal strain” measures how much it extends.
• Elasticity: A material’s degree of stretchability or pliability. While certain objects, like steel, rarely stretch at all, others, like rubber, are extremely elastic.
• Effects of Heat: Heat can alter the behaviour of materials. For an example, heat causes metal to expand. Because the material’s form varies with the temperature, that variation has an impact on the Poisson’s Ratio.

In order to determine the Poisson’s Ratio for substances in which heat is present, engineers apply mathematical expressions that include strain, elasticity, and the impact of temperature.

To explain how a material expands and contracts in all directions under all circumstances, they develop equations.

Poisson’s Ratio in thermodynamics, to put it briefly, is all about how materials react, stretch, and shrink in response to heat!

Derivation of Poisson’s Ratio from Fundamental Thermodynamic Principles

Poisson’s ratio is a figure that clarifies whether substances expand or contract in response to applied force. Consider extending a rubber band. It grows thinner as well as longer.

Poisson’s ratio is a measurement of the amount that it expands in one direction and compresses in another.

At this point, we may employ the fundamental concepts of thermodynamics—the study of heat, energy, and work—to understand this ratio.

Thermodynamics explains the flow and transformation of energy in materials. Energy flows within materials when we pull or squeeze them, altering their shape. We can understand why specific materials stretch or shrink by examining these energy shifts.

Thermodynamic mathematical equations are used by scientists to observe whether forces affect a material’s volume and shape.

They can calculate Poisson’s ratio using these. Understanding how pressures and energies fit together to explain how materials behave when they are pressed or pulled is similar to piecing together a puzzle.

In summary, we may better understand how materials change shape by applying the basic principles of thermodynamics, which brings us to the crucial parameter known as Poisson’s ratio.

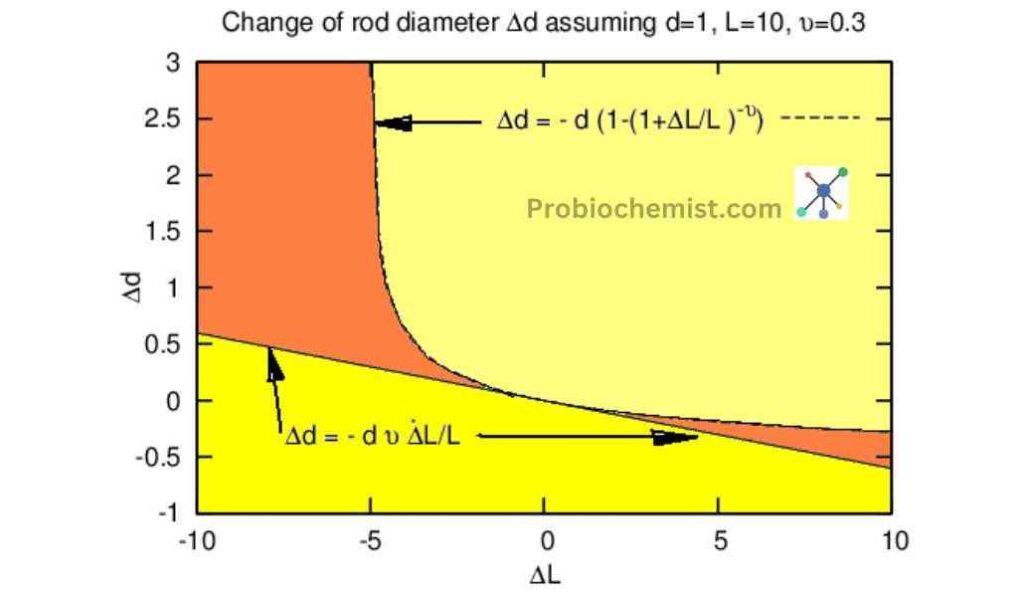
Derivation of Poisson’s Ratio for Elastic Materials in Thermodynamics

The Poisson’s ratio quantifies the behaviour of materials under compression or stretch. Just as when you pull on a rubber band, it grows thinner as it grows longer.

Poisson’s ratio has been in action there! It explains the connection between a material’s amount of stretching in one direction and shrinking in another.

The mathematical theory of thermodynamics emphasises on the properties of heat and energy, particularly how materials change shape in response to external influences.

In order to determine Poisson’s ratio, scientists employ mathematical and physical formulas and laws that describe precisely how different materials react to stress or pressure. They calculate the amount by which a material will contract in width upon lengthening.

Poisson’s ratio is a helpful instrument for engineering to figure out how elastic materials, such as the springs made of metal or rubber-based products, will respond to applied force.

When developing structures such as skyscrapers, bridges, or even basic toys, this is crucial! It guarantees the fact that under stress and pressure, materials won’t fracture or distort excessively.

Key Assumptions in the Derivation of Poisson’s Ratio

Poisson’s ratio is a figure that clarifies how materials expand or contract in response to force. When calculating Poisson’s ratio, we assume several crucial assumptions in thermodynamics, the study of heat and energy.

Among these fundamental presumptions are that the substance will act uniformly in every direction and the fact that the procedure will not significantly alter the temperature. Additionally, we presume that the substance is stable and not disintegrating.

Scientists can determine how a material will behave under pressure by using these assumptions, which helps to make structures like bridges and buildings safer!

The Role of Poisson’s Ratio in Thermodynamic Processes

The Poisson’s ratio is a measurement that indicates the behaviour of materials under stretching or compression. Pulling on a rubber band comes to mind.

The rubber band gets thinner in the middle as you stretch it. The total amount of thin it gets is explained by Poisson’s ratio.

The Poisson’s ratio is a crucial tool for figuring out how materials react to heat and fluctuations in energy that occur in thermodynamic processes.

As for an instance, Poisson’s ratio can be used to determine how much a material is going to expand when heated.

The ratio of Poisson’s is an essential instrument for scientists, technicians, builders, researchers and designers to forecast the behaviour of a material when it expands or contracts and its temperature changes at the same time.

We can create safer structures, bridges, and maybe even spaceships, rockets, missiles that can survive extreme temperature and pressure fluctuations without failing, just by knowing Poisson’s ratio! It’s a minor but crucial component in ensuring that while working with forces and heat, things function as they should.

Applications of Poisson’s Ratio in Thermodynamic

In order to figure out how things respond whenever temperature changes, Poisson’s Ratio can be useful in such a scenario.

Understanding Material Strength at Different Temperatures

We frequently discuss how materials respond under various conditions of pressure and temperature in thermodynamics.

Let us consider, for an example, a metal rod. It expands when heated, but scientists can forecast how much it will expand in various directions using Poisson’s ratio.

The material may lengthen, but it may also get thinner in the process. We can forecast this shift and ensure that components don’t break or deform in critical circumstances, such as in machinery or even buildings, by using Poisson’s Ratio.

Designing Structures to Handle Temperature Changes

We know that railway lines or train rails are composed of metallic items, they expand in hot weather.

The amount that they will expand in both directions—both in length and thickness—must be known by engineers. It would be dangerous if the tracks bent or broke due to their excessive expansion.

Scientists can forecast the behaviour of the metal and construct the tracks that will remain safe and stable even in extremely cold or hot conditions by employing Poisson’s Ratio Principle.

Engineers make use of this same idea to make aeroplanes, rockets, buildings and bridges!

Dealing with Pressure Changes in Gases and Liquids

Thermodynamics deals with liquids and gaseous substances in along with solids materials. Consider how air is blown into a balloon to see how it expands.

The balloon stretches in all directions due to the pressure created by the air inside. Scientists are able to clarify how materials respond when pressure changes through the application of Poisson’s Ratio, such as the rubber in the balloon.

Certain gases expand or shrink when they are heated or chilled. Manufacturers can create containers (such as petrol tanks) that won’t rupture when the gases inside them expand due to heat by using Poisson’s ratio.

Spacecraft and Extreme Environments

Both the temperature and the behaviour of materials can vary greatly from Earth to space, with extremes in temperature possible. Materials used in spacecraft must be able tolerate these harsh circumstances without failing.

Scientists can predict how various materials will react when their temperature variations in space cause them to broaden or constrict by using Poisson’s Ratio.

When constructing space shuttles, satellites, and space stations, for example, this understanding is essential. These vital responsibilities could not succeed if we have no knowledge how materials behave in various conditions!

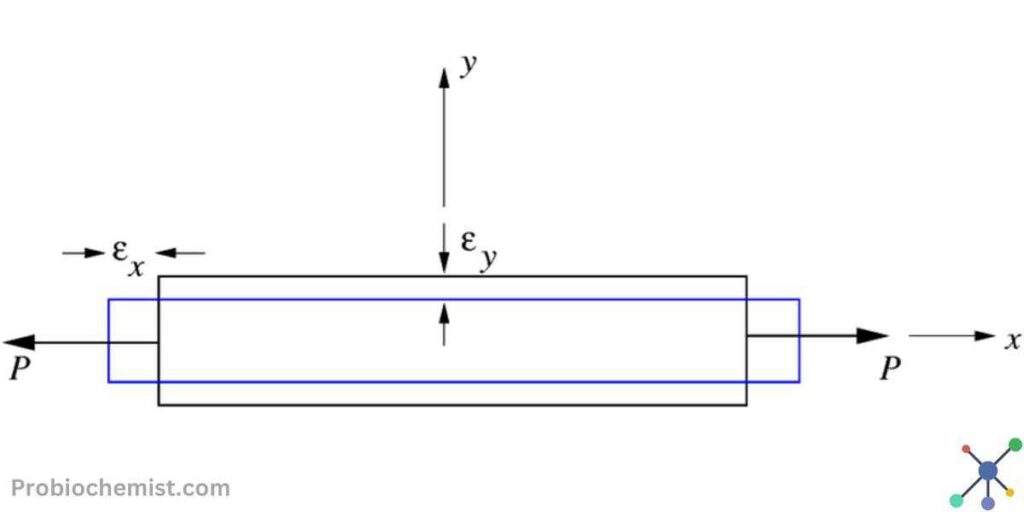
How Poisson’s Ratio Impacts Thermodynamic Equilibrium and Elasticity

In physics, a property known as Poisson’s ratio describes how materials respond to stretching or compressing. Assume you possess an elastic band. It becomes longer when you pull it, but it also becomes thinner.

We can determine how much narrower or broader something gets when it is stretched or compressed by using Poisson’s ratio.

Let’s begin by relating it to elastic properties and the equilibrium of thermodynamics. Thermodynamic equilibrium is akin to a balanced condition in which each of the forces are in equilibrium and absolutely nothing in a system is becoming cooler or warmer.

The capacity of a material to regain its former shape after being stretched or squeezed is known as its elasticity.

Since it affects the way substances react to these forces in thermodynamic equilibrium, Poisson’s ratio is very significant. For instance, when force exerted on a material with a high Poisson’s ratio alters shape more visibly.

This impacts its ability to stretch or the speed at which it returns to its initial shape, and it may even have an effect on how it maintains equilibrium within a system. It aids scientists in their understanding of how materials react under various circumstances and preserve equilibrium.

Poisson’s Ratio in Thermodynamics: Key Equations and Practical Examples

Poisson’s ratio is useful in measuring a material’s side-thinning effect.

The ratio can be described as the negative ratio of the axial strain, or how much the material changes in the direction that you pull or push, to the lateral strain, or how much the material moves sideways.

The Formula for Poisson’s Ratio is:

equation for Poisson’s ratio, V = − ^{Lateral Strain}/_{​Axial Strain}

Also, V = − ^ΔW/W/_ΔL/L

Where:

ΔW represents the change in width,

W represents the original width,

ΔL represents the change in length, and

L is the original length.

Key Equations

Bulk Modulus (K)

This evaluates how a substance reacts to constant pressure applied from all directions. Here’s the relationship to Poisson’s ratio:

K = ^E/_3(1−2v)

Here, K, which is dependent on the Poisson’s ratio, provides a measure of the amount of material compresed under pressure.

E represents Young’s modulus, and

ν is Poisson’s ratio.

Young’s Modulus (E)

This is an indicator of a material’s stiffness and is connected to Poisson’s ratio. The connection can be provided by:

E = 2G(1+ν)

E is Young’s modulus,

G is the shear modulus, and

ν represents Poisson’s ratio.

Practical Examples

• Rubber: Rubber has a Poisson’s ratio of about 0.5, which means that when the material is stretches out it just gets narrower and loses very little volume.
• Cork: The Poisson’s ratio of cork, which is used in the closure of wine bottles, is almost zero. It is unable to enlarge sideways when you push it. Because of this, it’s ideal for closing bottles because it holds its shape without expanding.
• Steel: The Poisson’s ratio of steel is approximately 0.3. Although it is somewhat elastic, it does not shrink or expand enough before breaking.

Effects of Temperature on Poisson’s Ratio in Thermodynamic Systems

A substance itself can react a different way whenever its operating temperature varies. As for example, it could grow and melt if it gets too hot.

Because the material expands or contracts more easily in these circumstances, the Poisson’s ratio could alter. Substances may stiffen at a lower temperature, therefore may also have an impact on how they alter size.

In real-world systems like engines, bridges, or even buildings, this is crucial. Understanding how materials respond to temperature fluctuations is essential for engineers to maintain system integrity and safety.

To put it simply, substances can act differently depending on their temperature, and this can affect their Poisson’s ratio, which allows us to measure such variations.

Poisson’s Ratio in Thermodynamics: Differences Between Solids, Liquids, and Gases

In the branch of science that studies about heat and energy known as thermodynamics, Poisson’s Ratio can behave somewhat differently for solids, liquids, and gases.

• Solids: Substances that are shaped clearly. Poisson’s Ratio can be calculated when a solid, such as an elastic band, is pressed or stretched. For the majority of part, solids swell out when squeezed and get slimmer when stretched. Poisson’s Ratios for solids typically range from 0 to 0.5.
• Liquids: Poisson’s Ratio does not hold true for them in the same manner. This is due to the fact that liquids are pliable and can flow in any direction. Squeezing a liquid causes it to expand out and vary its volume rather than behave like a solid, so an accurate Poisson’s Ratio cannot be determined.
• Gases: Somewhat like fluids, gaseous substances are shapeless and can expand to occupy an area. The volume of a gaseous substance changes when it is squeezed or expanded, but since gases can expand without restriction, we also don’t typically calculate Poisson’s Ratio in gaseous compounds.

The Relationship Between Poisson’s Ratio and Thermodynamic Properties of Solids

Poisson’s ratio relates with the behaviour of substances not only when they compress but also when they heat up and cooled down.

Poisson’s ratio can be affected by a material’s thermodynamic characteristics, such as its heat capacity and how it varies with temperature.

Let’s consider an example: the temperature of a substance might cause it to grow looser or harder. This influences how forces are applied and how they expand or compress.

Comprehending this correlation aids scientists in creating more resilient materials that can tolerate varying circumstances, such as variations in temperature or pressure, within apparatuses or structures.

To put it simply, thermodynamic parameters help us figure out how heat and temperature changes impact a substance’s reaction to compression, while Poisson’s ratio tells us how a material reacts to compression.

Theoretical Approaches to Poisson’s Ratio in Thermodynamic Fluid Dynamics

Scientists analyse Poisson’s ratio to learn more about how materials change shape under pressure or stretch.

Poisson’s ratio plays a crucial role in understanding the behaviour of fluids (such as water and air) in thermodynamic fluid dynamics, the study of how these materials react to variations in their pressure and temperature.

Mathematical methods for calculating Poisson’s ratio consist of predicting the behaviour of fluids and materials through mathematical and scientific representations.

By understanding the behaviour of anything from currents in the ocean to aeroplane wings, scientists can better create fluid-based technologies that are safe and effective.

Therefore, despite its complexity, it is useful for everyday objects that we see and use!

Poisson’s ratio in thermodynamics clarifies how materials undergo shape change under pressure. The amount that a material shrinks or extends in various directions when squeezed or stretched is explained by Poisson’s ratio.

These variations are related to energy, temperature, and other forces in thermodynamics through the derivation of Poisson’s ratio.

Knowing this makes it easier for engineers and scientists to forecast how certain materials will perform in diverse contexts, such as in vehicles, buildings, or even devices. So keep in mind that Poisson’s ratio provides an explanation why anything changes shape the next time you squeeze it!

I hope the article “Derivation for Poisson’s Ratio in Thermodynamics” is helpful for you! Let me know if you have any questions or need further clarification. Kindly share this article with ypur family and friends.